Determinan & Invers Matriks

Nama: Regina Ratna Dewita

Kelas: XI IPS 2

Absen: 24

Determinan Matriks

Determinan suatu matriks didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat ditentukan pada matriks persegi. Determinan dari matriks A dapat dituliskan det(A) atau |A|.

Untuk menentukan determinan dari sebuah matriks, terdapat dua aturan berdasarkan ordonya, yaitu ordo 2x2 dan ordo 3x3.

Determinan Matriks Ordo 2x2

Determinan matriks persegi dengan ordo 2x2 dapat dihitung dengan cara berikut:

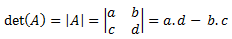
Determinan Matriks Ordo 3x3

Determinan matriks persegi dengan ordo 3x3 dapat dihitung dengan menggunakan dua cara, yaitu kaidah Sarrus dan ekspansi kofaktor. Namun, cara yang paling sering digunakan dalam menentukan determinan matriks ordo 3x3 adalah dengan kaidah Sarrus.

Langkah-langkah mencari determinan matriks ordo 3x3 dengan kaidah Sarrus:

1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan.
2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping.

|A| = (a.e.i) + (b.f.g) +( c.d.h) – (c.e.g) – (a.f.h) – (b.d.i)

|A| = (a.e.i + b.f.g + c.d.h) – (c.e.g + a.f.h + b.d.i)

Invers Matriks

Invers matriks adalah kebalikan (invers) dari sebuah matriks yang apabila matriks tersebut dikalikan dengan inversnya, akan menjadi matriks identitas. Invers matriks dilambangkan dengan A-1. Suatu matriks dikatakan memiliki invers jika determinan dari matriks tersebut tidak sama dengan nol.

Untuk menentukan invers dari sebuah matriks, terdapat dua aturan berdasarkan ordonya, yaitu ordo 2x2 dan ordo 3x3.

Invers Matriks Ordo 2x2

Invers matriks persegi dengan ordo 2x2 dapat dicari dengan cara sebagai berikut:

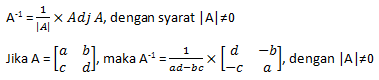
Invers Matriks Ordo 3x3

Untuk mencari invers matriks pada ordo 3x3, dapat digunakan metode eliminasi Gauss Jordan

.Secara sistematis, eliminasi Gauss Jordan dapat dinyatakan sebagai berikut:

Matriks persegi A dieliminasi menggunakan operasi aljabar sampai membentuk matriks identitas. Operasi yang dilakukan pada matriks A juga dilakukan pada matriks identitas sehingga jika matriks A sudah menjadi matriks identitas, maka matriks identitas akan berubah menjadi invers dari matriks A.

Soal Kontekstual

Arman membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?

Persoalan ini dapat diselesaikan menggunakan dua cara.

Jika maka dengan cara

Cara pertama, yakni cara invers, diperoleh .

Penyelesaian

Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)

5x + 3y = 11.500

4x + 2y = 9.000

Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni

Cara Pertama (Invers Matriks)

dan

Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500

Cara Kedua (Determinan Matriks)

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500.

Contoh Soal Determinan Matriks 2:

Contoh soal determinan matriks yang kedua ini punya angka yang sama dengan yang pertama, tapi cara yang diminta berbeda, yaitu dengan menggunakan metode minor-kofaktor.

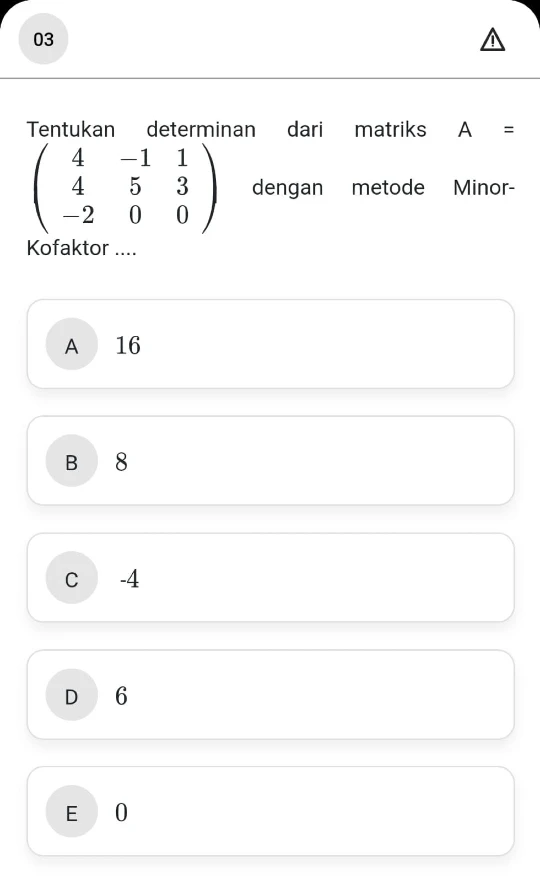
Pembahasan:

Oke, seperti yang udah gue jelasin tentang metode minor kofaktor di bagian rumus determinan matriks.

Cara pertama adalah elo lihat angka pada baris paling atas, kemudian ambil determinannya, jadinya akan seperti ini:

Determinan Matriks dan Metode Penyelesaiannya 106

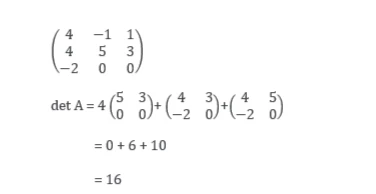
Contoh Soal Determinan Matriks 1:

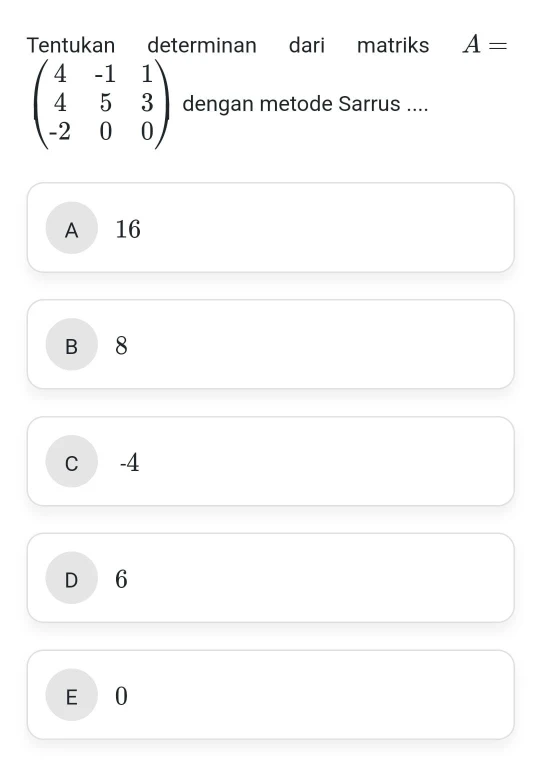
Pembahasan:

Dengan menggunakan metode Sarrus maka cara perhitungannya seperti elo menganyam (nama lain metode ini), yakni dengan menambahkan dua ruas di sisi kanan, seperti berikut:

Determinan Matriks dan Metode Penyelesaiannya 105

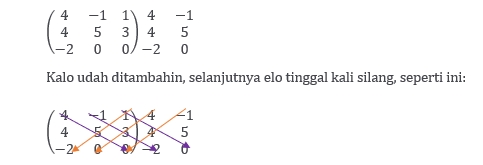
Arah panah ke kiri (panah orange) = -10, 0, 0

Arah panah ke kanan (panah ungu) = 0, 6, 0

Determinan adalah ruas kanan – ruas kiri = (0+6+0) – (-10+0+0) = 16

$AB^{-1} = \begin {bmatrix}-34 & 13 \\ 21 & -8 \end {bmatrix}$

Contoh soal 6 (Un 2018 IPS)

Diketahui matriks $A = \begin {bmatrix}1 & -2 \\ -1 & 3 \end {bmatrix}$ dan $B = \begin {bmatrix}2 & 1 \\ -1 & -1 \end {bmatrix}$ . Invers dari matriks AB adalah…

Pembahasan / penyelesaian soal

$AB = \begin {bmatrix}1.2 + -2.-1 & 1.1 + -2.-1 \\ -1.2+3.-1 & -1.1+3.-1 \end {bmatrix}$
$AB = \begin {bmatrix}4 & 3 \\ -5 & -4 \end {bmatrix}$

Selanjutnya diperoleh a = 4, b = 3, c = -5 dan d = -4, maka invers AB sebagai berikut:

$AB^{-1} = \frac {1}{4.-4 - 3.-5} \begin {bmatrix}-4 & -3 \\ 5 & 4 \end {bmatrix}$
$AB^{-1} = \begin {bmatrix}-4 & -3 \\ 5 & 4 \end {bmatrix}$

Contoh soal 7 (UN 2018 IPA)

Diketahui matriks $A = \begin {bmatrix}2 & 3 \\ 1 & 2 \end {bmatrix}$ dan $B = \begin {bmatrix}1 & 2 \\ -1 & 1 \end {bmatrix}$ . Matriks (AB)^-1 adalah…

Pembahasan \ penyelesaian soal

Hitung terlebih dahulu matriks AB seperti nomor 6 dan hasilnya sebagai berikut:

$AB = \begin {bmatrix}2.1+3.-1 & 2.2+3.1 \\ 1.1 + 2.-1 & 1.2 + 2.1 \end {bmatrix}$
$AB = \begin {bmatrix}-1 & 7 \\ -1 & 4 \end {bmatrix}$

Maka invers dari matriks AB adalah:

$AB^{-1} = \frac {1}{-1.4 - 7.-1} \begin {bmatrix}4 & -7 \\ 1 & -1 \end {bmatrix}$
$AB^{-1} = \frac {1}{3} \begin {bmatrix}4 & -7 \\ 1 & -1 \end {bmatrix}$

Contoh soal 8 (UN IPA 2018)

Diketahui matriks $A = \begin {bmatrix}-1 & 1 & 0 \\ 1 & -1 & 1 \end {bmatrix}$ dan $B = \begin {bmatrix}2 & 1 \\ 1 & -1 \\ 1 & 1 \end {bmatrix}$ . Jika matriks C = AB, invers C adalah C^-1 = …

Pembahasan / penyelesaian soal

Matriks C = AB sebagai berikut:

$AB = \begin {bmatrix}-1.2 + 1.1 + 0.1 & -1.1 + 1.-1 + 0.1 \\ 1.2 + -1.1 + 1.1 & 1.1 + -1.-1 + 1.1 \end {bmatrix}$
$AB = \begin {bmatrix}-1 & -2 \\ 2 & 3 \end {bmatrix}$

Maka invers C sebagai berikut:

$C^{-1} = \frac {1}{-1.3 - -2.2} \begin {bmatrix}3 & 2 \\ -2 & -1 \end {bmatrix}$
$C^{-1} = \begin {bmatrix}3 & 2 \\ -2 & -1 \end {bmatrix}$

Daftar Pustaka:

https://www.ilmusosial.id/2020/06/contoh-soal-cerita-matriks-dan.html

https://brainly.co.id/tugas/1476814

https://akupintar.id/info-pintar/-/blogs/matriks-pengertian-operasi-determinan-invers-dan-contoh-soal

https://www.google.com/amp/s/soalfismat.com/contoh-soal-invers-matriks-dan-pembahasannya/amp/

https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.zenius.net/blog/determinan-matriks&ved=2ahUKEwjijJrB3ZD5AhXmaGwGHbxYA8YQFnoECEAQAQ&usg=AOvVaw2eDOC3fQ6-ptHvJFqrOSmR

Cari Blog Ini

MY MATHEMATIC'S BLOG

Determinan & Invers Matriks

Komentar

Posting Komentar

Postingan populer dari blog ini

Barisan dan Deret

Integral Fungsi Aljabar

Program Linear